10623. Мысли наоборот

На плоскости расположено m эллипсов, n окружностей и p треугольников таким образом, что они делят ее на максимально возможное количество частей s. По заданному значению s вывести все такие возможные тройки чисел m, n, p, отсортировав их сначала по m, потом – по n.

Вход. Содержит не более 300 строк. Каждая строка содержит 32 - битовое знаковое число s – максимальное число частей, на которое могут разбить плоскость m эллипсов, n окружностей и p треугольников. Число s = -1 является концом входных данных и не обрабатывается. Известно, что 0 £ m, p < 100, 0 £ n < 20000.

Выход. Для каждого входного теста вывести его номер и все возможные тройки чисел m, n, p, отсортированные сначала по m, а затем – по n. Если ни одной тройки не существует, то вывести сообщение Impossible.

Пример входа

20
10
-1
 

Пример выхода

Case 1:

0 0 3

0 1 2

1 0 2

1 3 0

Case 2:

Impossible.

РЕШЕНИЕ

комбинаторика + перебор

Анализ алгоритма

Пусть n фигур разбивают плоскость на f(n) частей. Одна фигура разбивает плоскость на 2 части. Каждая следующая n - ая фигура должна иметь максимально возможное количество пересечений k с каждой из (n – 1) предыдущих фигур. Две окружности могут пересекаться максимум в двух точках (k = 2), два эллипса в четырех (k = 4), а два треугольника в шести (k = 6). Тогда

f(n) = f(n – 1) + k * (n – 1),

f(1) = 2

Решим рекуррентное уравнение:

f(n) = k * ((n – 1) + (n – 2) + … + 1) + 2 == k * + 2

Заметим, что f(0) = 1 для любого k (ноль фигур делят плоскость на одну часть).

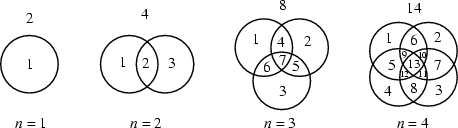
Окружности на плоскости

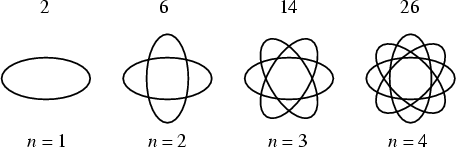
Эллипсы на плоскости

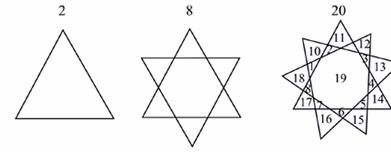
n = 1 n = 2 n = 3

Треугольники на плоскости

Из выше приведенной формулы следует, что m эллипсов, n окружностей и p треугольников могут разделить плоскость максимум на 2 + 2m (m – 1) + n (n – 1) + 4mn + 3p (p – 1) + 6pn + 6pm частей. m эллипсов и n окружностей могут иметь максимум 4mn точек пересечения, p треугольников и n окружностей или m эллипсов – соответственно 6pn и 6pm точек пересечения. Приравняем это значение к s и перепишем выражение как квадратное уравнение относительно n:

n² + n (4m + 6p – 1) + 2 + 2m (m – 1) + 3p (p – 1) + 6pm – s = 0

Если дискриминант уравнения является полным квадратом для некоторых целых m и p, 0 £ m, p < 100, то ищем соответственное неотрицательное значение n и проверяем его принадлежность интервалу 0 £ n < 20000. Остается перебрать все пары (m, p) из заданного интервала и для каждой из них решить квадратное уравнение. Найденные тройки остается упорядочить по заданному в условии задачи правилу.

Пример

Рассмотрим первый тест. На 20 частей плоскость можно разбить следующими комбинациями фигур: 3 треугольника, 1 окружность и два треугольника, 1 эллипс и два треугольника, 1 эллипс и две окружности.

Реализация алгоритма

Читаем входные данные и выводим номер теста CaseNo.

CaseNo = 1;

while(scanf("%d",&s), s > 0)

{

printf("Case %d:\n",CaseNo++);

Если входное значение s равно 1, то ответом будут три нуля:

if (s == 1)

{

printf("0 0 0\n");continue;

}

Введем переменную флаг found, который будет равен 1, если для заданного s будет найдена хотя бы одна тройка - решение. Изначально присвоим found значение 0.

found = 0;

Совершаем перебор всех возможных значений m, p (0 £ m, p < 100). По ходу вычисляем максимальное количество частей, на которое фигуры делят плоскость. Если на каком-то этапе значение суммы (res или res1) станет большей s, то выходим из цикла (нет смысла перебирать последующие значения соответствующей переменной).

for(m = 0; m < 100; m++)

{

res = 2 + 2 * m * (m - 1);

if (res > s) break;

mas.clear();

for(p = 0; p < 100; p++)

{

res1 = res + 3 * p * (p - 1) + 6 * m * p;

if (res1 > s) break;

Имеются значения m и p. Решаем приведенное выше квадратное уравнение относительно n. Вычисляем корень из дискриминанта det. Если дискриминант является полным квадратом (дробная часть числа det равна 0), то находим положительный корень уравнения n и проверяем его принадлежность интервалу 0 £ n < 20000. Для каждого m будем накапливать соответствующие пары – решения (n, p) в переменной mas типа вектор: vector<pair<int, int> > mas.

b = 4 * m + 6 * p - 1;

det = sqrt(1.0 * b * b - 4 * (res1 - s));

if (fabs(det - (int)det) < 1e-12)

{

n = (int)((-b + det) / 2);

if ((n < 0) || (n >= 20000)) break;

mas.push_back(make_pair(n,p));

}

}

Если для текущего значения m найдена хотя бы одна пара решений (n, p) (массив mas не пустой), то отсортировать и вывести все тройки – решения. Сортировка по умолчанию будет производиться по первому элементу пары (значению n).

if (mas.size())

{

sort(mas.begin(),mas.end());

for(i = 0; i < mas.size(); i++)

printf("%d %d %d\n",m,mas[i].first,mas[i].second);

found = 1;

}

}

Если решений не найдено, то вывести соответствующее сообщение.

if (!found) printf("Impossible.\n");

}